您的位置：获诺奖的“拓扑”：开启研究奇异物质大门
神秘的量子跃迁
实验的发展最终带来了一系列全新的物质状态需要得到解释。在1980年代，戴维和邓肯提出了一项突破性的理论，对先前有关材料导电性原理的理论提出了挑战。先前的相关理论最早是从1930年代开始发展的，经过几十年的发展，当时的主流观点认为相关理论已经非常完善。因此当在1983年戴维·索利斯证明先前的理论体系是不完善的，并且在低温条件下以及在强磁场环境下，需要引入一种全新的，基于拓扑原理的理论时，很多人都感到非常意外和惊讶。
在大约同一时期，邓肯·霍尔丹在对磁性原子链进行分析时，同样得到了一个非常相似，也同样出人意料的结果。他们的工作在随后新物质相的理论发展中起到了指导作用。戴维·索利斯利用拓扑学从理论上进行描述的神秘现象被称作“量子霍尔效应”。这一现象是在1980年由德国物理学家克劳斯·冯·克利青（Klaus von Klitzing）发现的，后者因为这项成就而获得了1985年度的诺贝尔物理学奖。克利青研究的是：在两块半导体之间放置一块导电薄层，当将温度降低到只有几K时并施以强大的磁场时，两层半导体材料之间的电子将会发生何种行为。在物理学中，当温度降低到很低的情况下，是很有可能出现一些极端情况的，比如说，很多材料在这种情况下出现磁性。这是因为此时材料内部的微型原子磁体都指向了相同的方向，从而产生了较强大的磁场，这一磁场可以被进行测量。然而，量子霍尔效应则更加难以理解，在半导体之间的导电层的电导率似乎只会呈现特定的数值，并且是几位精确的值，这样的情况在物理学中并不寻常。
测量显示，即便改变半导体的温度、磁场强度或者材料纯度，得到的结果都是一样的。当磁场变化达到一定程度，导电层的电导性也会出现相应变化，但这种变化不是连续的，而是跳跃的；如果降低磁场强度，导电层的电导性先是会非常精确地增加2倍，然后是3倍，然后是4倍，以此类推，都是一个个的整数。这种诡异的现象没有办法通过当时已有的理论进行解释，但运用拓扑学理论，戴维·索利斯对此给出了解释。
拓扑回答
拓扑描述了当一个对象被拉伸、扭曲或变形时保持不变的属性，而不是被撕裂。从拓扑层面讲，一个球和一个碗属于同一范畴，因为一个球形的粘土块可以转化成一个碗。但是，一个中间有孔的百吉饼（bagel）和手柄处有孔的咖啡杯就属于另一个范畴。当然，他们也可以被重塑成彼此的形状。因此，拓扑对象可以包含一个洞，或两个，或三个，或四个……但这个数字必须要是一个整数。这对于描述量子霍尔效应中存在的电导现象大有帮助，因为在量子霍尔效应的每步变化中唯一的变化就是一个整数的倍数变化。
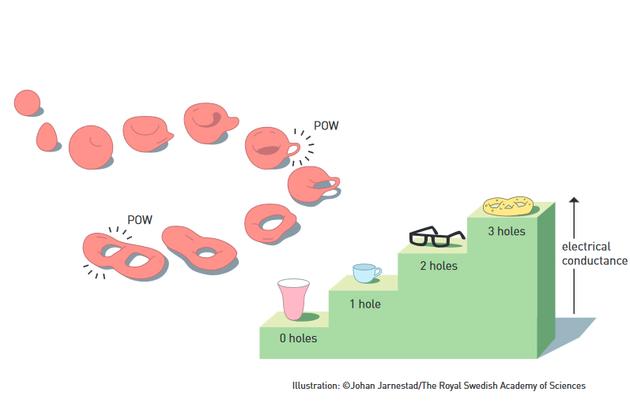拓扑。数学运算中这一分支的令人感兴趣之处在于其步进式变化属性，正如前文所述对象的孔的数量的变化。拓扑是此次诺贝尔物理学奖获得者所发现内容的关键，它解释了为什么电导率的变化是以整数步骤变化的。